Как-то мне попалась интересная Головоломка Лабиринт. Задача мне понравилась и было жалко ее просто решить и забыть. И я подумал - а что если решить эту задачу системно, по алгоритму, чтобы ответить на следующие вопросы:
- Есть ли вообще такой путь?
- Сколько таких путей?
- Как научить других решать похожие задачи?
Задание:
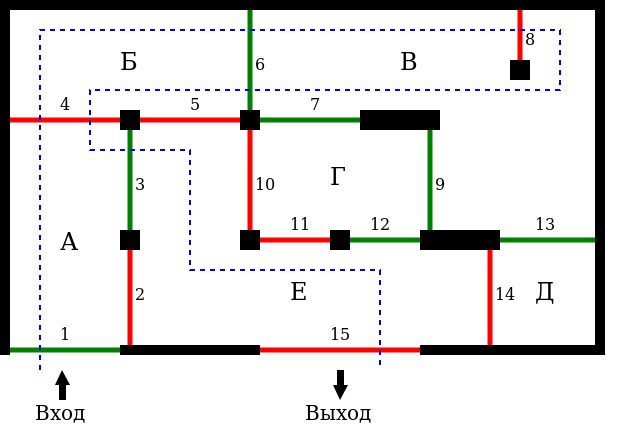
Вы входите в лабиринт в зеленый вход, а выйти нужно из красного выхода, при этом нельзя пересекать подряд две линии одного цвета.
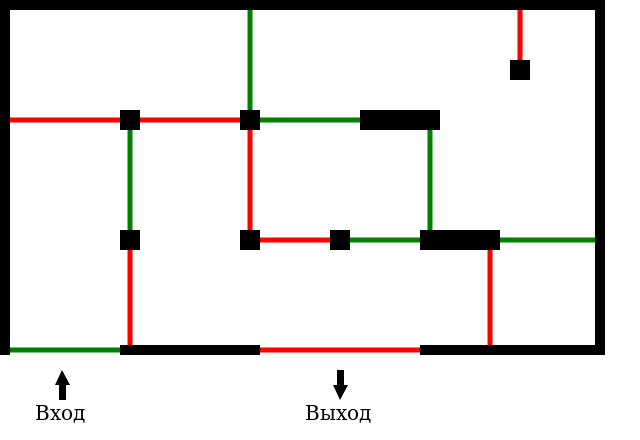
Итак, приступим.
Решение:
Прежде всего, нужно обозначить линии и комнаты.
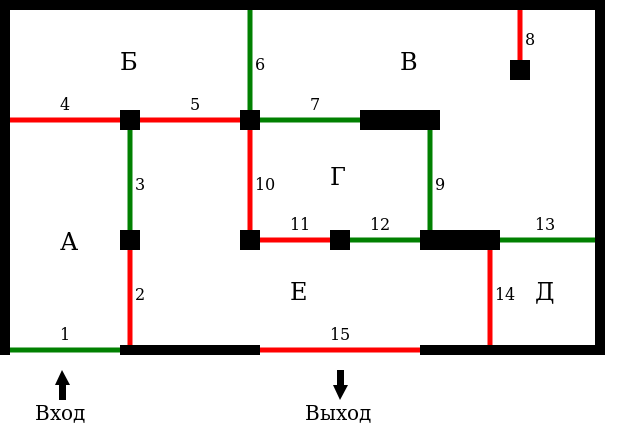
Обратите внимание:
- По условию задачи нельзя пересекать подряд две линии одного цвета, т.е. мы может пересекать только определенные линии и только в одном направлении.
- Допустим мы попали в комнату В из комнаты Б через зеленую линию 6. Мы не можем ни вернуться назад через линию 6, ни пересечь зеленые линии 7, 9 и 13. Мы может только пересечь отдельно стоящую красную линию 8. И если мы ее пересечем мы остаемся в той же комнате В, но в новом состоянии и теперь можем пересекать зеленые линии 6, 7, 9 и 13. Т.е. в каждой комнате мы можем находится в двух состояниях: зеленом или красном.
Идя от Входа и пересекая зеленую линию 1, мы попадаем в комнату А в зеленом состоянии (Азел). Будем записывать это так:
Вход --1-> Aзел
Т.к. теперь нельзя пересекать зеленые линии, мы можем только пересечь или красную линию 2, чтобы попасть в комнату Е в красном состоянии (Екр), или красную линию 4, чтобы попасть в комнату Б в том же красном состоянии (Бкр). Запишем это так:
Aзел --2-> Eкр
Aзел --4-> Бкр
Теперь, используя нотацию выше, методично проходим по всем комнатам и записываем куда мы можем пройти в зеленом и красном состоянии. Т.е. в каждой комнате нужно представить, что мы зашли туда вначале через зеленую линию и записать возможные переходы через красные линии, а потом, что мы зашли туда же через красную линию и записать возможные переходы через зеленые линии. Ничего сложного, требуется только внимание и аккуратность!
Комната А:
Aзел --2-> Eкр
Aзел --4-> Бкр
Акр --3--> Eзел
Комната Б:
Бзел --4--> Акр
Бзел --5--> Екр
Бкр --6--> Взел
Комната В:
Взел --8--> Вкр
Вкр --6--> Бзел
Вкр --7--> Гзел
Вкр --9--> Гзел
Вкр --13--> Дзел
Комната Г:
Гзел --10--> Екр
Гзел --11--> Екр
Гкр --7--> Взел
Гкр --9--> Взел
Гкр --12--> Езел
Комната Д:
Дзел --14--> Екр
Дкр --13--> Взел
Комната Е:
Езел --10--> Гкр
Езел --11--> Гкр
Езел --14--> Дкр
Езел --15--> Выход
Екр --3--> Азел
Екр --12--> Гзел
Теперь рисуем схему переходов. Каждое состояние рисуем как зеленый или красный эллипс, каждую линию как зеленую или красную стрелку с соответствующим номером линии.
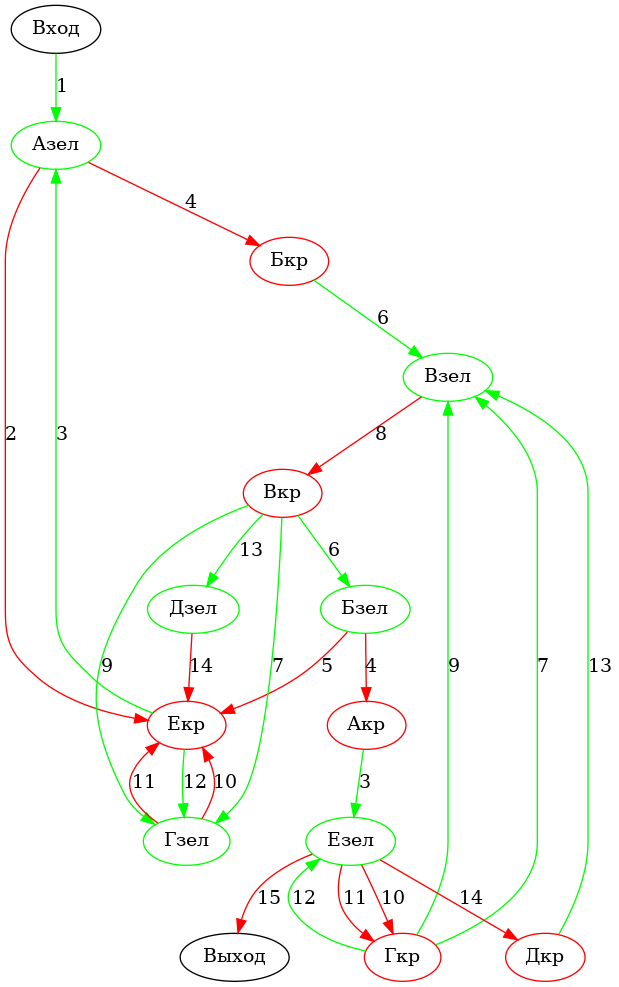
Обратите внимание:
В зеленые состояния входят только зеленые стрелки и выходят только красные, а в красные состояния входят только красные стрелки и выходят только зеленые. Также, если мы следуем по стрелкам, то у нас все время чередуются цвета. Такая вот графическая отладка получилась.
Самая трудная часть позади. Теперь осталось только найти путь. Начинаем с Выхода и двигаемся ко Входу. Смотрим какие стрелки ведут к Выходу. Только одна красная стрелка 15 из Езел. Записываем 15. Дальше смотрим какие стрелки ведут в Езел. Только одна зеленая стрелка 3 из Акр. Записывает 3. И так далее. В итоге у нас должна получиться следующая последовательность:
15 3 4 6 8 6 4 1
Перевернув которую мы получаем искомый путь:
1 4 6 8 6 4 3 15
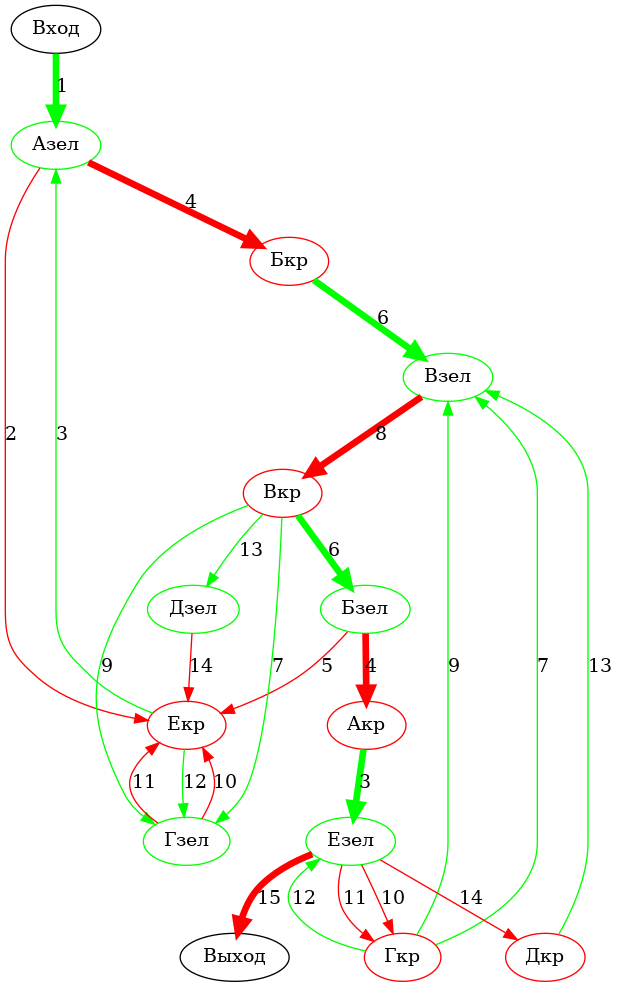
И вот найденное решение:
Теперь можно ответить на вопросы:
-
Есть ли вообще такой путь?
Да, есть.
-
Сколько таких путей?
Путь единственный.
-
Как научить других решать похожие задачи?
С помощью этого алгоритма можно искать выход из большого числа лабиринтов. Обозначаем комнаты как эллипсы, а переходы как стрелки, если можно идти только в одном направление или просто линии, если можно возвращаться. Для большого лабиринта вы просто тратите больше времени на составление его схемы. Если вы где-то ошиблись, всегда можно вернуться к каждому шагу по отдельности и проверить его правильность. Теперь можно написать программу, которая будет искать выход из лабиринта.
В заключении, для полноты следует добавить, что мы использовали математическую модель ориентированного графа, который к тому же оказался двудольным, и решение задачи свели к поиску пути от Входа до Выхода в этом графе.
Надеюсь, у меня получилось и кто-то из вас узнал что-то новое.